统计究竟能否研究因果问题?¶
统计学史拾遗
天才的高斯在研究天文学时,首次引进了最大似然和最小二乘的思想,并且导出了正态分布(或称高斯分布)。其中最大似然有些争议,比如 Arthur Dempster 教授说,其实高斯那里的似然,有贝叶斯或者信仰推断(fiducial inference)的成分。高斯那里的 “统计” 是关于 “误差” 的理论 ,因为他研究的对象是 “物理模型” 加“随机误差”。
大约在 100 多年前,Francis Galton 研究了父母身高和子女身高的 “关系”,提出了“(向均值)回归” 的概念。众所周知,他用的是线性回归模型。此时的模型不再是严格意义的“物理模型”,而是“统计模型” — 用于刻画变量之间的关系,而不一定是物理机制。
之后,Karl Pearson 提出了“相关系数”(correlation coefficient)。后世研究的统计,大多是关于 “相关关系” 的理论。 但是关于 “因果关系” 的统计理论,非常稀少。
据 Judea Pearl 说,Karl Pearson 明确地反对用统计研究因果关系;有意思的是,后来因果推断为数不多的重要文章(如 Rosenbaum and Rubin 1983; Pearl 1995)都发表在由 Karl Pearson 创刊的 Biometrika 上。
统计学一直以来研究的都是相关性问题,用它来研究因果是比较危险的。
相关性不等于因果性,相关性不等于因果性,相关性不等于因果性!!!重要的事情说三遍!
否则,会有很多荒唐的结论,这个网站Correlation is NOT Causation收集了一些spurious correlations。
例如,缅因的离婚率和美国的人造黄油消耗高度相关:
辛普森悖论¶
另一个著名的例子是辛普森悖论(Yule Simpson's paradox):
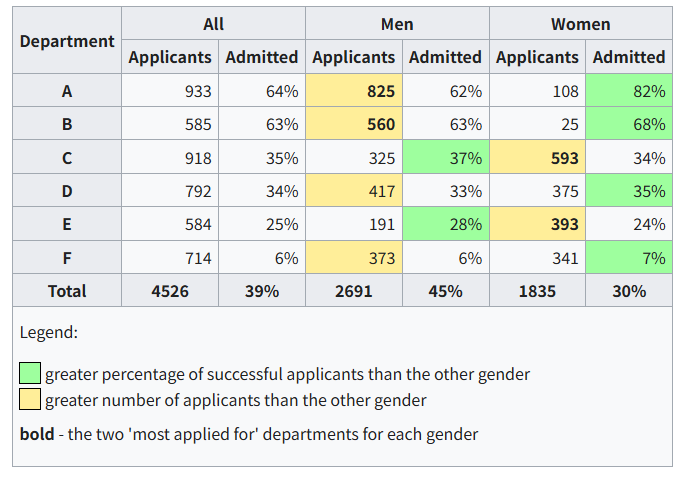
UC Berkeley在1973的招生情况如下:
| 男 | 女 | |
|---|---|---|
| 录取 | 3714 | 1512 |
| 未录取 | 4728 | 2809 |
| 录取率 | 44% | 33% |
可以看到,男性的录取率高达44%,比女性的33%高了九个百分点,这难道不是性别歧视?集美们这能忍??
然而当我们把视角转换到院系(上图展示了六个人数最多的院系),就可以发现在大多数的院系(A、B、D、F),女生的录取率都更高。在整个UC Berkeley的85和院系中,有4个院系女性的录取率显著地低于男性,有6个院系男性的录取率显著地低于女性。
这难道不是性别歧视?集帅们这能忍??
原因¶
那么到底存不存在性别 -> 录取的因果关系呢?如果不存在,为什么会造成这样现象呢?
graph LR
性别 --?--> 录取答案自然是不存在性别歧视。之所以出现了男性总体录取率更高的原因是:男性偏向于选择那些录取率更高的院系。
仔细观看分院院系的录取情况你会发现,录取率排名第一和第二的院系,女性申请者反而很少。录取率低得多的CDEF院系,女性申请者反而很多。
原来是有另外一个变量(院系选择)在捣鬼,造成了虚假相关性。这被称为混杂效应。
graph LR
院系 --> 性别
院系 --> 录取现实世界中,这种情况无处不在。从纯粹的数学上来看,这就是一个初等的不等式性质:
$$ \frac{a}{b} \lt \frac{c}{d}\quad \frac{a'}{b'} \lt \frac{c'}{d'} $$ 然而 $$ \frac{a+a'}{b+b'} \gt \frac{c+c'}{d+d'} $$
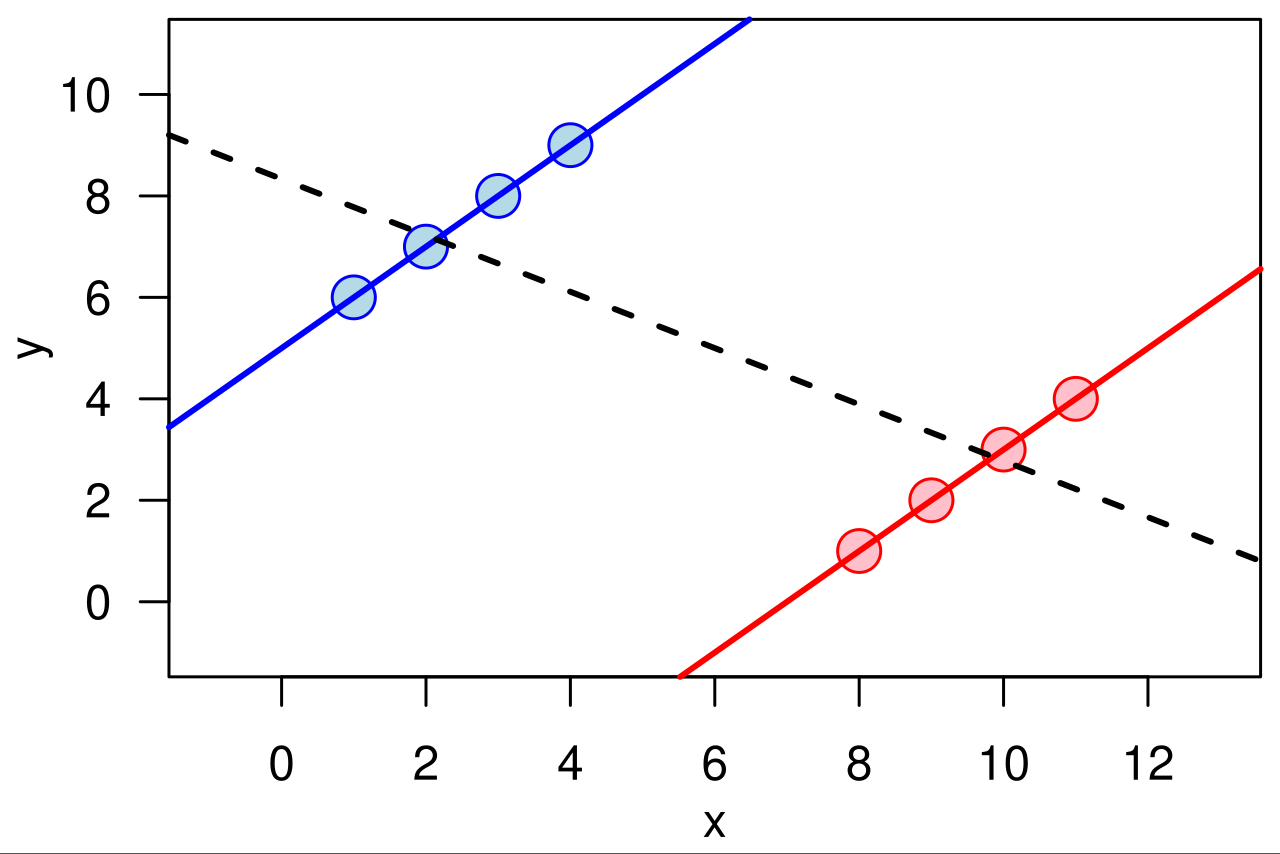
维基百科上有一张图,也可以很直观地帮助我们理解辛普森悖论的产生:
可以看到,xy在红色数据集和蓝色数据集中都各自呈现正相关,然而总体上却呈现负相关。背后就是“红蓝分组”这个变量在作祟。
如何寻找因果¶
从上面的例子可以看到,简单的列联表统计是不能给出具有说服力的因果关系的,反而会带来一些令人迷惑的悖论。
线性回归也不可靠,甚至可能得出相反的结论。
这俩工具没了,传统统计学一半的理论都无用了。
因此想要探究因果关系,需要非常小心的建模、考证。请看下一节,常用的因果推断方法。
创建日期: 2025-03-22 01:28:32
广告
人要恰饭的嘛🤑🤑