铺瓷砖¶
给定一个大小为 n x m 的长方形,返回贴满矩形所需的整数边正方形的最小数量。
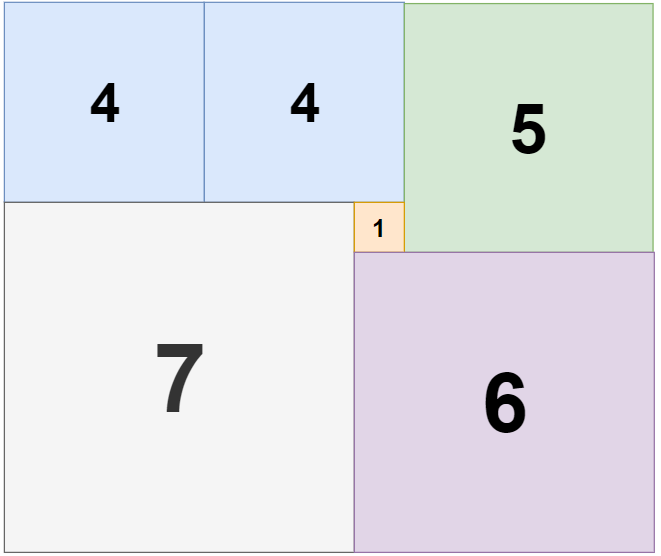
例如下图是n=11, m=13的一个解:
题解¶
题目很短,但是一点也不简单。
一个朴素的上界¶
这个问题是一个经典NP完全问题,我们没有很好的多项式解法。不过我们可以很容地估计出这个问题的一个上界。
考虑这样一个贪心算法:
- 对于m等于n的情况,返回1
- 对于m不等于n的情况,我们优先用一个最大的正方形(也就是边长为
min(n,m)的正方形)
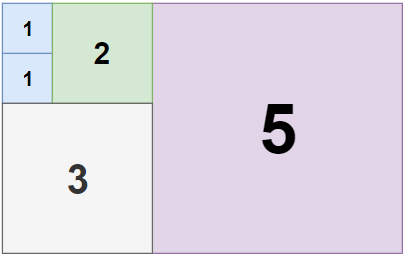
这个贪心算法可以很好的解决下面的case:
代码写起来也很简单(甚至可以稍微优化一下,消解掉递归):
def naive(i,j):
if i==j:
return 1
elif i>j:
return 1+naive(i-j,j)
else:
return 1+naive(i,j-i)
回溯算法¶
既然没有好算法,只能暴力搜索+剪枝了。
核心的想法是把这个问题想象为为填格子,维护一个指针(i,j):它代表我们现在所处的位置、一个数组filled:它代表我们已经完成的填充、一个计数变量t:它代表我们已经使用的正方形数量:
- 从
(0,0)开始 - 如果
(i,j)已经被填充过了,就跳过,移动到(i,j+1)- 我们从左上角开始移动
(i,j),如果移动到了行末就从下一行的开头继续 - 这样我们可以保证
(i,j)之前的所有格子都被填充过了
- 我们从左上角开始移动
- 如果
(i,j)没被填充,那么就递归搜索所有可能的填充方法- 考虑一个边长为w的正方形(w的范围很容易计算)
- 它会填充
(i,j) - (i+w-1,j+w-1) - 填充完毕之后,我们从
(i,j+w)开始继续移动指针即可
- 递归结束之后,我们进行回溯
- 把之前填充过的所有正方形范围内的格子都标记为未填充即可
下面的代码来自Leetcode全解,应该是搞信息竞赛的朋友写的,用了很多二进制数字的技巧:
def tilingRectangle(n: int, m: int) -> int:
def dfs(i: int, j: int, t: int):
nonlocal ans
if j == m:
i += 1
j = 0
if i == n:
ans = t
return
if filled[i] >> j & 1:
dfs(i, j + 1, t)
elif t + 1 < ans: # 这个剪枝几乎是无效的
r = c = 0
for k in range(i, n):
if filled[k] >> j & 1:
break
r += 1
for k in range(j, m):
if filled[i] >> k & 1:
break
c += 1
mx = r if r < c else c
for w in range(1, mx + 1):
for k in range(w):
filled[i + w - 1] |= 1 << (j + k)
filled[i + k] |= 1 << (j + w - 1)
dfs(i, j + w, t + 1)
for x in range(i, i + mx):
for y in range(j, j + mx):
filled[x] ^= 1 << y
ans = n * m
filled = [0] * n
dfs(0, 0, 0)
return ans
我自己改了一个更容易懂的版本(并且加入了额外的剪枝操作,可以极大地加快搜索效率):
def f(n,m):
# naive的解法可以给出一个简单的上界估计
# 从而在后续的搜索中进行剪枝
def naive(i,j):
if i==j:
return 1
elif i>j:
return 1+naive(i-j,j)
else:
return 1+naive(i,j-i)
def dfs(i,j,t):
# filled和ans都是闭包外的变量
# 其中filled是递归搜索的状态之一,需要不断更新
# 而ans用于剪枝和返回最终答案
nonlocal ans, filled
# 如果到了行末,就进入下一行
if j==m:
i+=1
j=0
# 如果i==n说明已经完全填满,可以结束搜索
if i==n:
ans = t
return
# 如果这个格子已经填充,就跳到下一个
if filled[i][j]:
dfs(i, j+1, t)
# 否则需要递归搜索
### 注意这里我们使用了剪枝,不考虑比naive上界大的情况
elif t+1 < ans:
r = c =0
# 水平方向允许的最大正方形边长
for k in range(m-j):
if filled[i][j+k]:
break
c += 1
# 竖直方向允许的最大正方形边长
for k in range(n-i):
if filled[i+k][j]:
break
r += 1
mx = min(r,c) # min max就是整体允许的最大正方形
for w in range(1,mx+1):
# 添加一个边长为w到正方形
# 从 i,j 到 i+w-1, j+w-1 都标记为filled
for x in range(w):
for y in range(w):
filled[i+x][j+y] = 1
# 接着递归,指针移动到之前添加的正方形后面
dfs(i, j+w, t+1)
# 回溯
# 去掉之前添加的所有正方形
for x in range(i, i + mx):
for y in range(j, j + mx):
filled[x][y] = 0
filled = [[0 for _ in range(m)] for _ in range(n)]
# 从粗略的上界出发,进行带剪枝的回溯搜索
ans = naive(n,m)
dfs(0,0,0)
return ans
性能对比¶
这里给出带剪枝和不带剪枝的性能对比。
我用此前的两个代码分别求解了1<=n<m<15的所有解:
def gen_ans(k=15):
from time import time
t1 = 0
t2 = 0
for n in range(1,k+1):
for m in range(n,k+1):
s = time()
a1 = f(n,m)
t1 += time()-s
s = time()
a2 = tilingRectangle(n,m)
t2 += time()-s
assert a1 == a2
return t1,t2
gen_ans(). # (22.43414831161499, 43.80258631706238)
结果显示,额外的剪枝操作带来了一倍的效率提升。
好诶!
最后更新: 2025-08-11 17:50:22
创建日期: 2025-08-11 17:50:22
创建日期: 2025-08-11 17:50:22
广告
人要恰饭的嘛🤑🤑