跳转至

排序数组

给你一个整数数组 nums，请你将该数组升序排列。

题解

排序问题是算法中最经典的问题之一了。

通常排序可以在数组、链表等数据结构上进行，不同数据结构上相同算法也可能有不同的性质。

本题考查的是数组的排序，较为简单。链表的排序要困难得多，请看Leetcode 148: 排序链表。

Quote

本文大部分内容和所有的图片均来自：

这里仅仅是个人学习笔记，如有需要请看一手资料～

评价维度

排序算法可以从以下几个纬度进行评价：

  • 时空复杂度：这是所有算法都需要考虑的指标
    • 基于比较的排序算法的时间复杂度下限是$\mathcal{O}(n\log(n))$
    • 当然也有其他类型的排序，计数排序就不是基于比较的排序，可以突破这个下限
  • 稳定性：相同元素的相对顺序不变就称为稳定排序
    • 基数排序、计数排序、插入排序、冒泡排序、归并排序是稳定排序。
    • 选择排序、堆排序、快速排序、希尔排序不是稳定排序。
  • 原地排序：在原始的数据结构进行排序，这样通常更快，更节省内存

选择排序

  • 时间复杂度： $\mathcal{O}(n^2)$
  • 空间复杂度：$\mathcal{O}(1)$
  • 数组的选择排序是不稳定的，而链表的选择排序通常是稳定的

选择排序的核心想法非常简单：不断把最小的数字放到已经排序好的数组的末尾。

  • 本质上，我们是在从左到右像玩蜘蛛纸牌一样安排所有的数字
  • 先找最小的，然后找次小的，以此类推

选择排序的代码如下：

def selection_sort(a):
    n = len(a)
    for i in range(n):
        ith = i
        # 在a[i]之后的所有元素中找到最小的那一个，和a[i]交换
        for j in range(i + 1, n):
            if a[j] < a[ith]:
                ith = j
        a[i], a[ith] = a[ith], a[i]
    return a

冒泡排序

  • 时间复杂度： $\mathcal{O}(n^2)$
  • 空间复杂度：$\mathcal{O}(1)$
  • 冒泡排序是稳定的

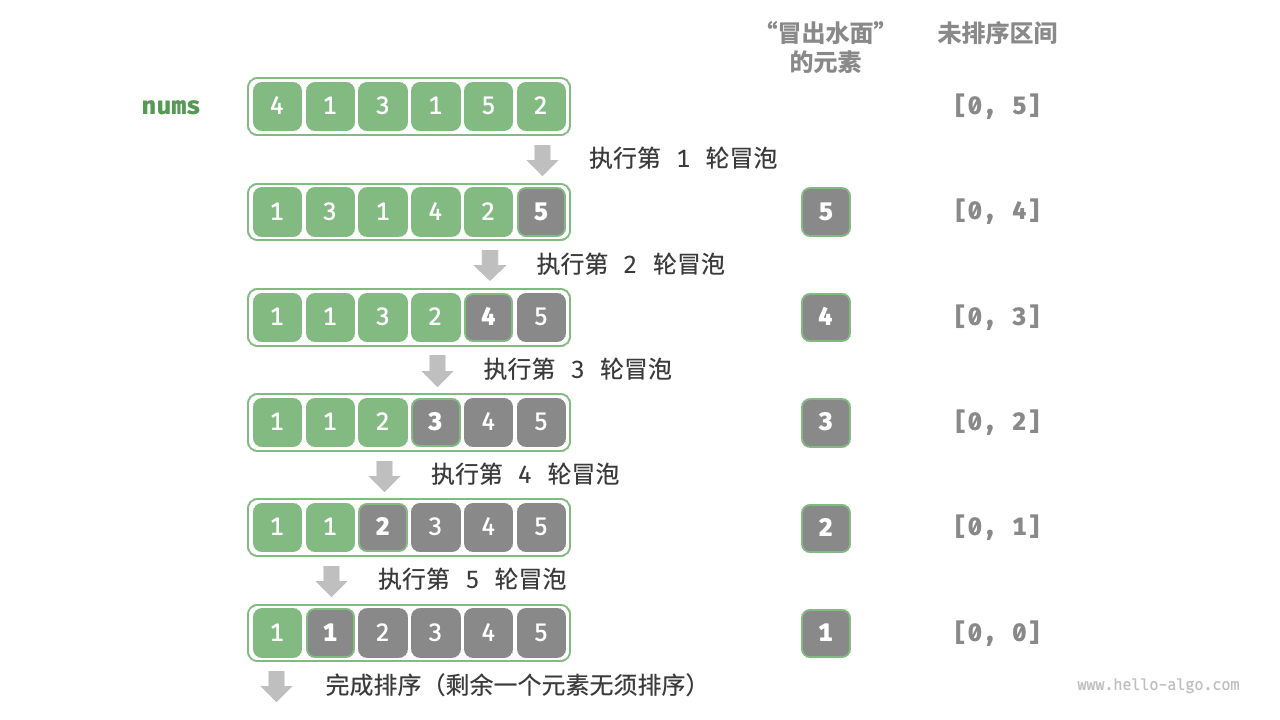
冒泡排序的想法也很简单：不断遍历数组，交换逆序，直到不存在逆序。

冒泡排序的代码如下：

def bubble_sort(a):
    n = len(a)
    while 1:
        # 这个flag用于终止循环
        no_reverse = True
        for i in range(n-1):
            # 如果存在逆序
            if a[i] > a[i + 1]:
                # 就交换，并且这是flag为False
                no_reverse = False
                a[i], a[i + 1] = a[i + 1], a[i]
        if no_reverse:
            break
    return a

插入排序

  • 时间复杂度： $\mathcal{O}(n^2)$
  • 空间复杂度：$\mathcal{O}(1)$
  • 插入排序是稳定的

插入排序的想法也是很直观的：遍历数组，不断把未排序的部分插入到已排序的部分。

代码如下：

def insertion_sort(a):
    n = len(a)
    for i in range(1, n):
        # 待插入的值
        key = arr[i]
        # 往左找插入的地方
        j = i - 1
        while j >= 0 and arr[j] > key:
            # 整体往右挪挪
            arr[j + 1] = arr[j]
            j = j - 1
        # 插入我们的数字
        arr[j + 1] = key
    return a

这里第十行挪数字的操作需要注意，我举个例子（之前的图中）：

  • 4,[1], 3 , 1 , 5 , 2，现在要插入1
  • 1, 4 ,[3], 1 , 5 , 2，现在要插入3
    • 我们遍历3的左侧
    • 左侧第一个是4，比3大
      • 往右挪一挪：1,4,4,1,5,2
    • 左侧第二个是1，比3小
      • 可以插入：1,3,4,1,5,2
  • 1, 3 , 4 ,[1], 5 , 2
  • 1, 1 , 3 , 4 ,[5], 2
  • 1, 1 , 3 , 4 , 5 ,[2]
  • 1, 1 , 2 , 3 , 4 , 5

计数排序

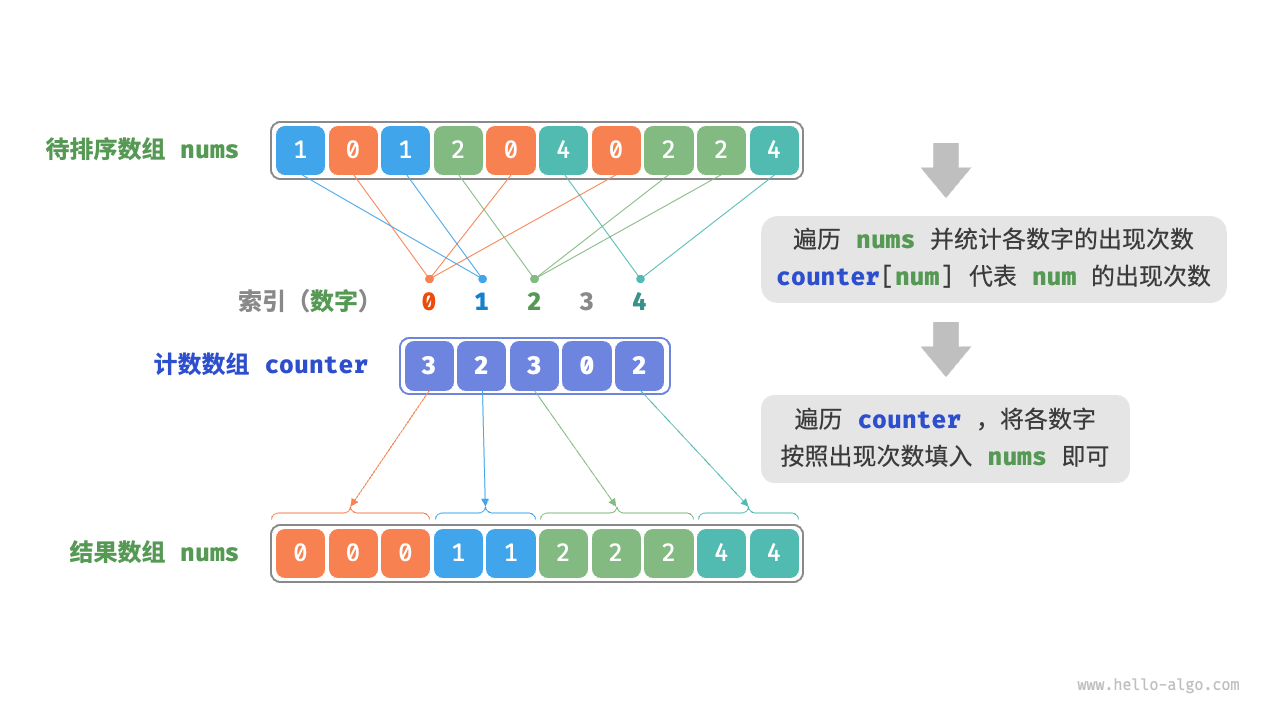
计数排序（counting sort）通过统计元素数量来实现排序，通常应用于自然数数组。

  • 时间复杂度： $\mathcal{O}(n+m)$，其中$m$是待排序数据的值域范围大小
  • 空间复杂度：$\mathcal{O}(n+m)$
  • 计数排序是稳定的

计数排序的想法如下：

可以看到，用下标计数的操作要求待排序数组的元素都是自然数

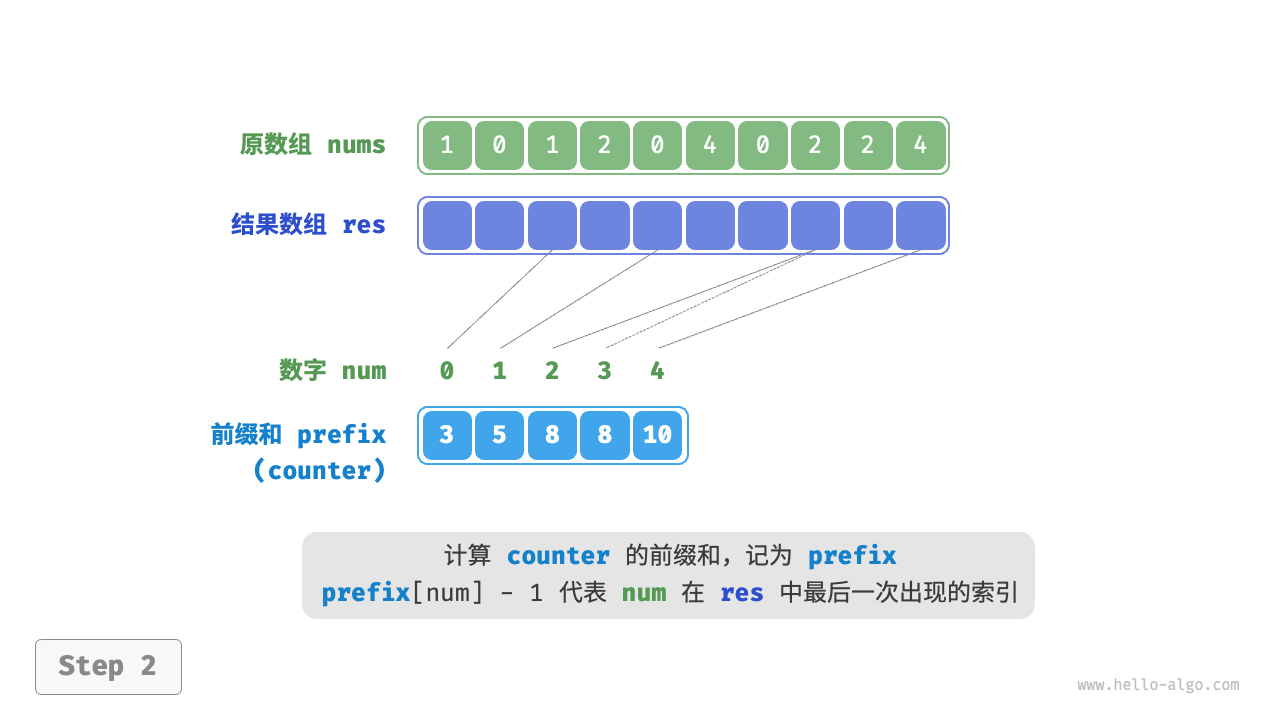
为了保持排序的稳定性，我们使用前缀和的技巧，直接得到每一个取值所在的最后一个位置：

然后从右往左生成排序好的数组即可。代码如下

def counting_sort(a):
    n = len(a)
    m = max(a)
    cnt = [0] * (m+1)
    b = [0] * n
    # 计数
    for i in range(n):
        cnt[a[i]] += 1
    # 计算前缀和，代表某个取值所在的最后一位
    for i in range(1,m+1):
        cnt[i] += cnt[i - 1]
    # 生成排序好的数组
    for i in range(n-1, -1, -1):
        num = a[i]
        b[cnt[num]-1] = a[i]
        cnt[num] -= 1
    return b

快速排序

  • 时间复杂度： $\mathcal{O}(n\log(n))$，我们终于突破了$\mathcal{O}(n^2)$
  • 空间复杂度：看情况，最多$\mathcal{O}(n)$
  • 数组快速排序是不稳定的

快速排序（英语：Quicksort），又称分区交换排序（英语：partition-exchange sort），简称「快排」，是一种被广泛运用的排序算法。

快速排序的过程如下，核心策略就是分治：

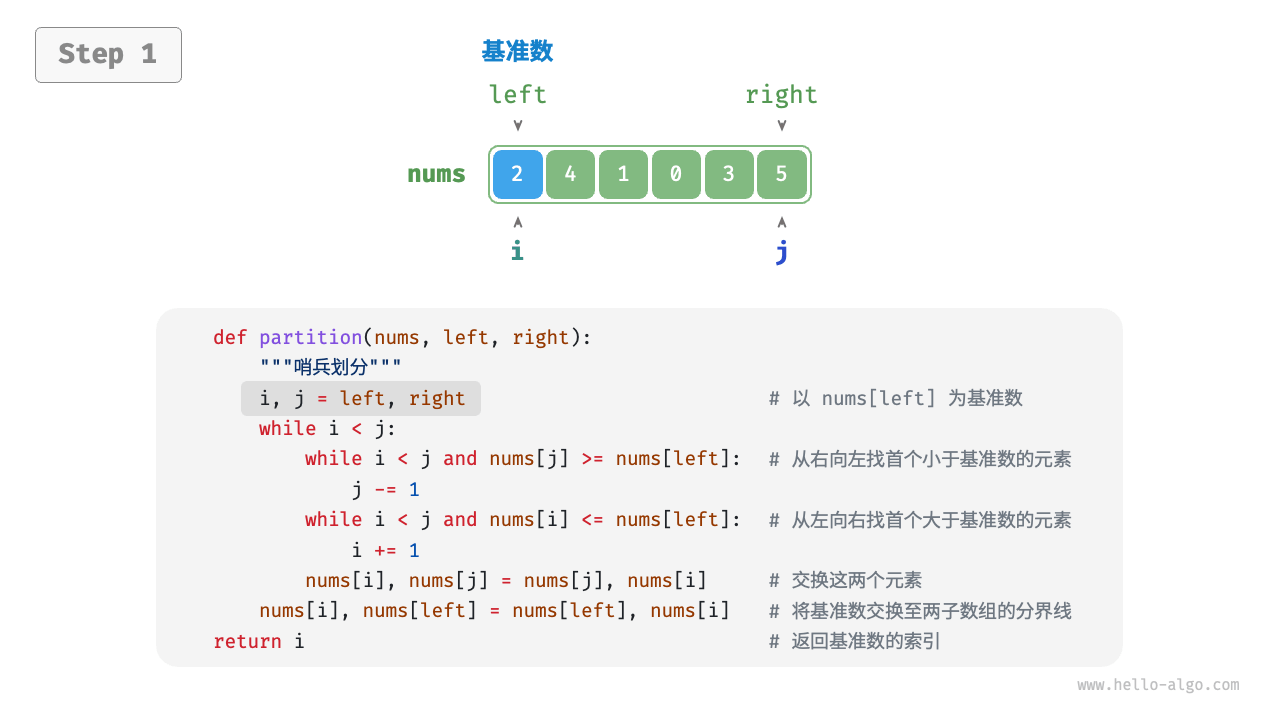
可以看到，其中一个关键的算法就是partition，它是一种双指针算法，可以快速把数组划分为两个部分。

完整的算法实现如下：

def partition(a, l, r):
    i,j = l,r
    x = a[l] # 划分点
    while i<j:
        # 右侧往左找一个更小值
        while i<j and a[j]>=x:
            j -= 1
        # 左侧往右找一个更大值
        while i<j and a[i]<=x:
            i += 1
        # 交换
        a[i],a[j] = a[j],a[i]
    # i,j 相遇，划分已经完成
    # 把划分点交换到中间
    a[l],a[i] = a[i],a[l]
    return i

def _quick_sort(a, l, r):
    if l >= r:
        return
    i = partition(a, l, r)
    _quick_sort(a, l, i - 1)
    _quick_sort(a, i + 1, r) # 可能出现：i+1 >= r

def quick_sort(a):
    _quick_sort(a, 0, len(a)-1)
    return a

Warning

注意，上面高亮的两行不可以交换顺序。

由于初始化的划分点在左侧，我们必须要首先移动右侧的指针。

例如数组[1,2]，我们初始化的划分点为x=1，i=0, j=1，如果先移动左侧的指针，左右指针会在i=j=1的位置相遇，然后和我们的划分点交换，最终数组变成[2,1]，排序出错了！！

先移动右侧的指针就不会有这个问题。

一个更加精简的版本是：

最好记的版本
def quick_sort(a, l, r):
    if l >= r:
        return
    x = a[l]
    i,j = l, r
    while i < j:
        while i < j and a[j] >= x:
            j -= 1
        while i < j and a[i] <= x:
            i += 1
        a[j], a[i] = a[i], a[j]
    a[l], a[i] = a[i], a[l]

    quick_sort(a, l, i - 1)
    quick_sort(a, i + 1, r)
另外一个版本 

def quick_sort(a, l, r):
    if l >= r:
        return
    x = a[l]
    i,j = l, r
    while i < j:
        while i < j and a[j] >= x:
            j -= 1
        a[i] = a[j]
        while i < j and a[i] <= x:
            i += 1
        a[j] = a[i]
    a[i] = x
    quick_sort(a, l, i - 1)
    quick_sort(a, i + 1, r)
这个版本中，我们把交换左右元素的操作拆分了。

我们首先把a[l]的值保存在x中（然后这个位置就是空闲的了，可以放入其他的数字），然后进入while循环。

上面两个版本虽然也能实现快排，但是必须以数组第一个元素作为基准点开始递归，可能会出现退化的情况。

退化情况

快速排序的最差的时间复杂度是$\mathcal{O}(n^2)$，如果数组已经排好序或者元素全部相同就会退化到这个复杂度。

为了减缓这个情况，我们可以随机选取划分点：

最高效的版本
def quick_sort(a, l, r):
    if l >= r:
        return
    # 随机初始化一个划分点
    x = a[randint(l, r)]
    # i和k同时从l出发，k跑的快（如果遇到了和x相等的值i不往前走）
    i, k, j = l, l, r
    while k <= j:
        # 如果遇到比x小的数字a[k]，就和a[i+1]交换（换言之，放到左侧）
        if a[k] < x:
            a[i], a[k] = a[k], a[i]
            i, k = i + 1, k + 1
        # 如果遇到比x大的数字，就放到右侧
        elif a[k] > x:
            a[j], a[k] = a[k], a[j]
            j -= 1
        # 否则啥也不干继续往前走
        else:
            k = k + 1
    # a[i:j+1]都是等于x的值
    # 所以只需要排序这个区间外侧
    quick_sort(a, l, i - 1)
    quick_sort(a, j + 1, r)

当然，我们还可以把前面的代码稍作修改，使得它从随机的基准点开始：

def quick_sort(a, l, r):
    if l >= r:
        return
    p = random.randint(l,r+1)
    a[p],a[l] = a[l],a[p] # 随机选一个，交换到左侧即可
    x = a[l]
    i,j = l, r
    while i < j:
        while i < j and a[j] >= x:
            j -= 1
        while i < j and a[i] <= x:
            i += 1
        a[j], a[i] = a[i], a[j]
    a[l], a[i] = a[i], a[l]

    quick_sort(a, l, i - 1)
    quick_sort(a, i + 1, r)

不过在Leetcode上这个代码依然会超时，因为它无法处理元素全部相同的情况（退化到$\mathcal{O}(n^2)$）。

当然，如果可以使用额外的空间，快排还可以写的更简单：

import random

def quick_sort(arr):
    # 如果数组长度小于等于1，直接返回
    if len(arr) <= 1:
        return arr
    # 随机选择一个基准点
    pivot = random.choice(arr)
    # 将数组分为三部分：小于基准、等于基准、大于基准
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    # 递归排序左右两部分，然后合并
    return quick_sort(left) + middle + quick_sort(right)

这个代码可以通过Leetcode

归并排序

  • 时间复杂度： $\mathcal{O}(n\log(n))$
  • 空间复杂度：$\mathcal{O}(n)$
  • 归并排序是稳定的

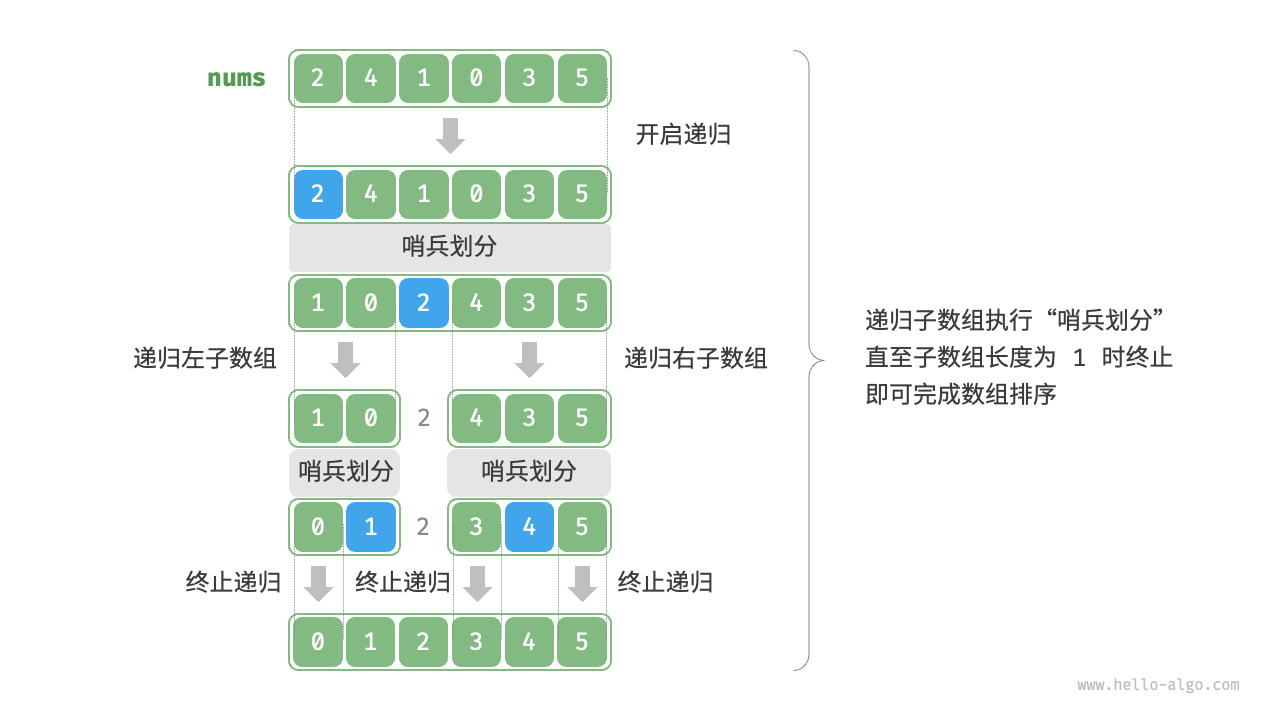
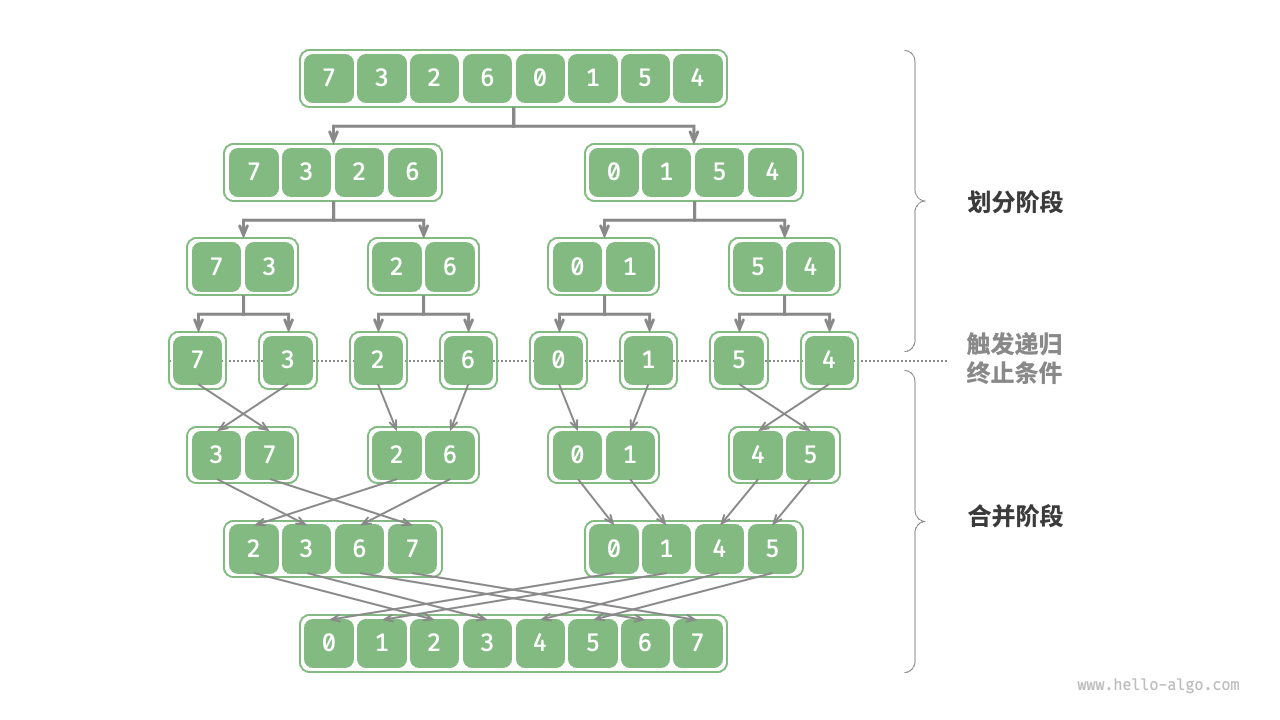
归并排序的思想也是分治，并且比快速排序还要更极端、更彻底：

可以看到，归并排序的思想就是简单粗暴地把数组一分为二，直到数组只有一个元素（这时候数组显然是有序的）。然后利用额外的空间合并两个有序数组。

Info

由于归并排序是简单粗暴的二分，实际上无论我们要排序的数组是什么样子它都可以稳定地工作，时间复杂度保持$\mathcal{O}(n\log(n))$。

这是快速排序不具备的特点。就拿Leetcode 912来说，如果你写了一个简单的快速排序算法，大概率会在一些算例超时，因为快速排序最差的时间复杂度是$\mathcal{O}(n^2)$（例如已经排序好的数组，或者元素全都相同的数组）。

归并排序的代码如下：

def _merge_sort(a, l, r):
    # 数组长度为1，停止递归
    if l==r:
        return
    m = (l+r)//2
    # 否则把数组一分为二，进行递归
    _merge_sort(a, l, m)
    _merge_sort(a, m+1, r)
    # 递归结束之后，左侧两个子数组都是有序的了，需要进行合并
    tmp = [] # 使用额外空间辅助合并
    i,j = l,m+1
    while i<=m or j<=r: # 还有数字没被放进tmp
        # 左侧数字被放完了
        # 或者
        # 左侧数字没放完，右侧数字也没放完，但是右侧的更小
        if (i>m) or (j<=r and a[j] < a[i]):
            # 放入右侧的数字
            tmp.append(a[j])
            j += 1
        # 否则放入左侧的数字
        else:
            tmp.append(a[i])
            i += 1
    a[l:r+1] = tmp

def merge_sort(a):
    _merge_sort(a, 0, len(a)-1)
    return a

这段代码最巧妙的就是第16行的条件，需要记一下。

其他排序算法

还有其他常见的排序算法：

  • 堆排序
    • 堆排序（英语：Heapsort）是指利用 二叉堆 这种数据结构所设计的一种排序算法。堆排序的适用数据结构为数组。
  • 桶排序
    • 桶排序（英文：Bucket sort）是排序算法的一种，适用于待排序数据值域较大但分布比较均匀的情况。
  • 基数排序
    • 基数排序（英语：Radix sort）是一种非比较型的排序算法，最早用于解决卡片排序的问题。基数排序将待排序的元素拆分为 k 个关键字，逐一对各个关键字排序后完成对所有元素的排序。
  • 希尔排序
  • Tim排序：一种混合的、稳定的排序算法，这是Python的默认排序算法。

不再一一展开。

最后更新: 2025-08-14 22:32:20
创建日期: 2025-08-14 22:32:20

广告

人要恰饭的嘛🤑🤑

评论