刷题常用数据结构¶
之前练习过Python内置的各种数据结构(字典、列表、集合、元组、整型等),但这远远不够。刷Leetcode的过程中还有一些常用的逻辑数据结构需要掌握,总结如下。
逻辑数据结构?¶
逻辑数据结构区别于物理数据结构,它是计算机系统中抽象出的对象,描述的是数据模型,关系着我们如何访问、修改数据。
逻辑数据结构和物理数据结构的区别?
好的,这是一个非常核心的计算机科学概念。我们来详细、清晰地解释逻辑数据结构和物理数据结构,以及它们之间的区别和联系。
TL;DR¶
- 逻辑数据结构:关注数据的 “是什么” 和 “为什么”。它定义了数据元素之间的抽象关系,以及可以在这些数据上执行的操作。它是面向用户和应用程序的。
- 物理数据结构:关注数据的 “怎么样” 和 “在哪里”。它定义了数据在计算机内存(如RAM)或存储设备(如硬盘)中的实际存储方式、布局和访问方法。它是面向计算机系统的。
逻辑数据结构¶
逻辑数据结构是从逻辑或概念的角度来看待数据是如何组织和管理。它不关心数据具体存储在内存的哪个地址,只关心数据元素之间的逻辑关系。
主要特点:
- 抽象性:描述的是模型,而非具体实现。
- 操作导向:定义了一组可以在该结构上执行的操作(如插入、删除、查找、遍历)。
- 关注关系:核心在于数据元素之间的逻辑关系(前驱、后继、父子、键值对等)。
常见类型:
- 线性结构:元素之间存在顺序的一对一关系。
- 数组:元素在逻辑上是连续的顺序表。
- 链表:元素通过指针连接,逻辑上连续,但物理上可以不连续。
- 栈:后进先出(LIFO)的线性表。
- 队列:先进先出(FIFO)的线性表。
- 非线性结构:元素之间存在一对多或多对多的关系。
- 树:具有层次关系的结构(如二叉树、B树、堆)。
- 图:由顶点和边组成的任意关系网络。
- 集合:没有明显顺序关系的一组元素。
- 哈希表:通过键(Key)直接访问值(Value)的映射结构。
例子:
当你使用编程语言声明一个 List 或 Map 时,你就是在使用逻辑数据结构。你只关心它能存数据、能按顺序访问(List)或能通过键取值(Map),而不关心它在内存里是怎么存的。
物理数据结构¶
物理数据结构是逻辑数据结构在计算机存储介质上的具体实现。它决定了数据实际存储在内存中的方式,如何分配内存空间,以及如何通过地址来访问数据。
主要特点:
- 具体性:涉及具体的内存地址、指针、偏移量、块、页等。
- 效率导向:设计的核心目标是提高存储效率、访问速度和减少内存碎片。
- 依赖硬件:其性能会受到存储介质特性(如内存的随机访问 vs 硬盘的顺序访问)的影响。
常见类型:
- 连续存储:
- 数组:在内存中分配一块连续的空间来依次存储所有元素。这是逻辑数组最常见的物理实现。
- 链式存储:
- 链表:每个元素(节点)分散存储在内存的不同位置,每个节点不仅包含数据,还包含指向下一个节点地址的指针(或引用)。
- 索引存储:建立附加的索引表,通过索引项来定位数据记录的实际地址(如数据库中的B+树索引)。
- 散列存储:根据元素的关键字,通过哈希函数计算出其物理存储地址。
区别与联系¶
| 特征维度 | 逻辑数据结构 | 物理数据结构 |
|---|---|---|
| 核心关注点 | 数据元素之间的抽象关系和操作 | 数据在存储介质上的具体布局和访问方法 |
| 视角 | 用户/程序员视角(做什么) | 系统/实现视角(怎么做) |
| 性质 | 抽象的,独立于平台和语言 | 具体的,依赖于硬件和语言 |
| 目标 | 解决问题、建模、提供清晰的API | 优化性能、节省空间、管理内存 |
| 例子 | List, Stack, Tree, Graph, Map | 连续内存块、指针链接、索引文件、数据页 |
其中最重要的一点:一种逻辑数据结构可以有多种物理实现。选择哪种物理实现取决于你对性能的需求(读写速度、内存开销等)。
经典例子:
-
逻辑结构 “线性表” 可以有多种物理实现:
-
使用连续存储(数组):
- 优点:随机访问速度快(通过下标直接计算地址,时间复杂度O(1))。
- 缺点:插入和删除需要移动大量元素(时间复杂度O(n)),大小固定(静态数组)或动态扩容有成本。
- 使用链式存储(链表):
- 优点:插入和删除效率高(只需修改指针,时间复杂度O(1)),大小可灵活动态变化。
- 缺点:随机访问效率低(需要从头遍历,时间复杂度O(n)),每个节点有额外的指针空间开销。
- 使用其它方式(如动态数组):
- 例如 Java 中的
ArrayList或 C++ 中的std::vector,它们在逻辑上是一个可以动态增长的“数组”。其物理实现通常是一块连续内存,当空间不足时,会分配一块更大的新内存,将旧数据拷贝过去。它平衡了数组和链表的一些优缺点。
- 例如 Java 中的
另一个例子是逻辑结构 “图”,它的物理实现可以是:
- 邻接矩阵(一个二维数组)
- 邻接表(一个数组+多个链表)
- 十字链表 等
总结¶
理解逻辑和物理数据结构的区别是成为优秀程序员的关键一步。
- 当你设计程序和解决问题时,你主要思考逻辑结构:“我需要一个先进先出的队列来处理这些任务” 或 “我需要一棵树来表示公司的组织结构”。
- 当你优化性能和进行底层开发时,你必须考虑物理结构:“我这个频繁按索引访问的列表,应该用数组而不是链表来实现” 或 “为了减少内存碎片,我需要一个自定义的内存分配器”。
简单来说,逻辑结构是蓝图,物理结构是具体的建筑施工方案。同一张蓝图(如“一栋100层的摩天大楼”),可以根据不同的地质条件、预算和材料,有多种不同的施工方案(物理实现)。
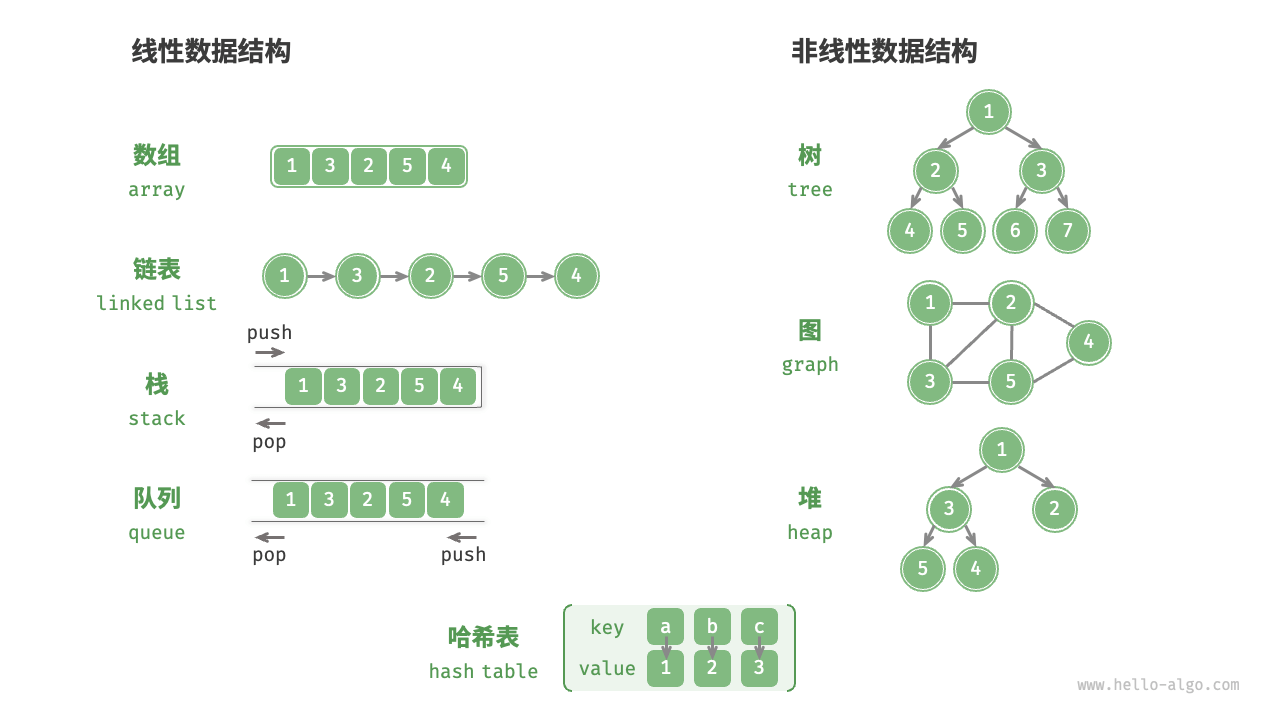
常见的逻辑数据结构有下面几种:
图源:Hello算法
练习题¶
栈¶
栈是一种后进先出(LIFO)的线性表,在Python中可以用列表很方便地实现栈:
stack = []
stack.append(x) # 压栈
y = stack.pop() # 弹栈
单调栈¶
单调栈是特殊的栈,它还要求维护元素是有序的(我们只需要在压栈的时候拿待压栈的元素和栈顶元素比较即可)。
队列¶
队列是一种先进先出(FIFO)的线性表,在Python中可以用列表很方便地实现队列。
queue = []
queue.insert(0, x) # 入队
y = queue.pop() # 出队
当然Python标准库也有一个队列实现:queue.py,通常用于多线程消息分发:
import threading
import queue
q = queue.Queue()
def worker():
while True:
item = q.get()
print(f'Working on {item}')
print(f'Finished {item}')
q.task_done()
# 启动工作线程。
threading.Thread(target=worker, daemon=True).start()
# 向工作线程发送三十个任务请求。
for item in range(30):
q.put(item)
# 阻塞直到所有任务完成。
q.join()
print('All work completed')
双端队列¶
双端队列就是两边都可以入队、出队的队列。Python中可以用列表来模拟,也可以用标准库中的实现:
from collections import deque
q = deque()
# api如下
q.append(x)
q.appendleft(x)
y = q.pop()
y = q.popleft()
单调队列¶
单调队列就是单调的队列,可以用双端队列实现。
链表¶
链表是一种依赖指针实现的线性数据结构,逻辑上是连续的表但是物理上往往不连续。
图¶
Note
图是一种非线性的数据结构,由点和边组成。有专门的图论研究图的性质和算法。图可以建模很多问题是最常用的数据结构之一。
树¶
树是一种非线性的数据结构,也是一种特殊的图。无向、无环、连通的图就是一棵树。
当然还有其他等价的刻画,例如
|V|=|E|-1的连通图就是树、极大无环图是树、极小连通图是树。
显然,链表是退化的树。
二叉树¶
二叉树是一类常用的树,它的每个节点最多只有两个分叉。满足特定性质的二叉树我们起了名字:
- 完美二叉树(perfect binary tree):所有层的节点都被完全填满,也叫满二叉树。
- 完全二叉树(complete binary tree):仅允许最底层的节点不完全填满,且最底层的节点必须从左至右依次连续填充。
- 完满二叉树(full binary tree):除了根节点,其他节点都有两个叶子节点。
- 平衡二叉树(balanced binary tree):任意节点的左子树和右子树的高度之差的绝对值不超过 1 。
二叉搜索树¶
二叉搜索树是特殊的二叉树,其节点顺序为严格全序关系,它要求:对于每个节点设它的值为x,左子树所有节点的值都比x小,右子树所有节点的值都比x大。
二叉搜索树可以在对数时间内完成搜索。不过极端情况下二叉搜索树可能会比较偏(甚至退化为链表),因此各种平衡二叉树被提出,例如:AVL树、红黑树。
树状数组¶
Note
树状数组也叫Fenwick Tree,是一种特殊的数组,可以高效处理前缀查询(进而区间查询)问题。具体的实现方法可以看最长递增子列的题解。
下标 (Index): 1 2 3 4 5 6 7 8
原始数组 (A): [A1] [A2] [A3] [A4] [A5] [A6] [A7] [A8]
树状数组 (C): [C1] [C2] [C3] [C4] [C5] [C6] [C7] [C8]
管辖关系:
C[1] = A[1]
C[2] = A[1] + A[2]
C[3] = A[3]
C[4] = A[1] + A[2] + A[3] + A[4]
C[5] = A[5]
C[6] = A[5] + A[6]
C[7] = A[7]
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
线段树¶
线段树是树状数组的升级版,是真正的二叉树而非依赖数组实现。能用树状数组解决的问题,用线段树都可以。
一个完全二叉树,每个阶段负责一个区间:
[1-8]
/ \
[1-4] [5-8]
/ \ / \
[1-2] [3-4] [5-6] [7-8]
/ \ / \ / \ / \
[1] [2] [3] [4] [5] [6] [7] [8]
哈希表¶
哈希表通过一个哈希函数,将键映射到一个数组中的特定位置,从而可以在平均情况下以常数时间复杂度 O(1) 进行插入、删除和查找操作。Python中的字典就是哈希表。
堆¶
堆(heap)是一种树,每个节点的键值都大于等于其父亲键值的堆叫做小根堆,否则叫做大根堆。一般我们说的堆都指二叉堆,换言之它背后是一颗完全二叉树。
优先队列¶
Note
优先队列是一种特殊的队列,它不遵守先进先出(FIFO)的原则,而是在入队的时候携带一个优先级,出队的时候优先级最高的会先出队。优先队列通常用堆来实现,因此也叫堆队列。Python的标准库中有一个实现:heapq.py
from heapq import heappush, heappop
pq = []
heappush(pq, x) # 入队
y = heappop(pq) # 出队
创建日期: 2025-08-20 18:48:56
广告
人要恰饭的嘛🤑🤑